On the Properties of Path Additions for Traffic Routing

Abstract

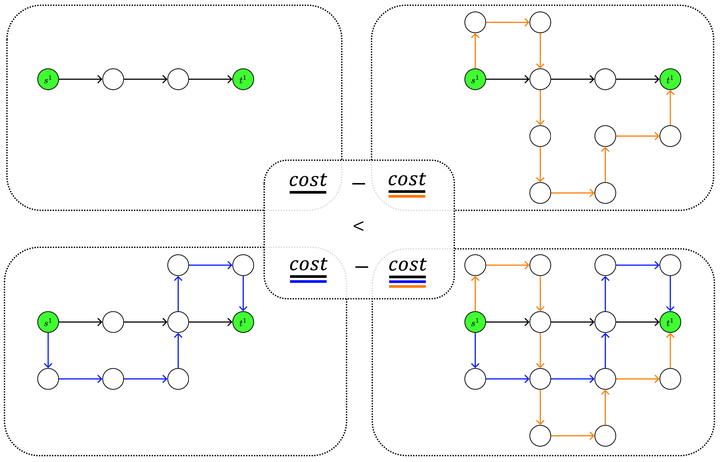
In this paper we investigate the impact of path additions to transport networks with optimised traffic routing. In particular, we study the behaviour of total travel time, and consider both self-interested routing paradigms, such as User Equilibrium (UE) routing, as well as cooperative paradigms, such as classic Multi-Commodity (MC) network flow and System Optimal (SO) routing. We provide a formal framework for designing transport networks through iterative path additions, introducing the concepts of trip spanning tree and trip path graph. Using this formalisation, we prove multiple properties of the objective function for transport network design. Since the underlying routing problem is NP-Hard, we investigate properties that provide guarantees in approximate algorithm design. Firstly, while Braess’ paradox has shown that total travel time is not monotonic non-increasing with respect to path additions under self-interested routing (UE), we prove that, instead, monotonicity holds for cooperative routing (MC and SO). This result has the important implication that cooperative agents make the best use of redundant infrastructure. Secondly, we prove via a counterexample that the intuitive statement “adding a path to a transport network always grants greater or equal benefit to users than adding it to a superset of that network” is false. In other words, we prove that, for all the routing formulations studied, total travel time is not supermodular with respect to path additions. While this counter-intuitive result yields a hardness property for algorithm design, we provide particular instances where, instead, the property of supermodularity holds. Our study on monotonicity and supermodularity of total travel time with respect to path additions provides formal proofs and scenarios that constitute important insights for transport network designers.

Matteo Bettini

PhD Candidate

Matteo’s research is focused on studying heterogeneity and resilience in multi-agent and multi-robot systems.

Amanda Prorok

Professor

Amanda’s research focuses on multi-agent and multi-robot systems. Our mission is to find new ways of coordinating artificially intelligent agents (e.g., robots, vehicles, machines) to achieve common goals in shared physical and virtual spaces.